
This means that almost 75% of the students scored lower than George and only 25% scored higher.
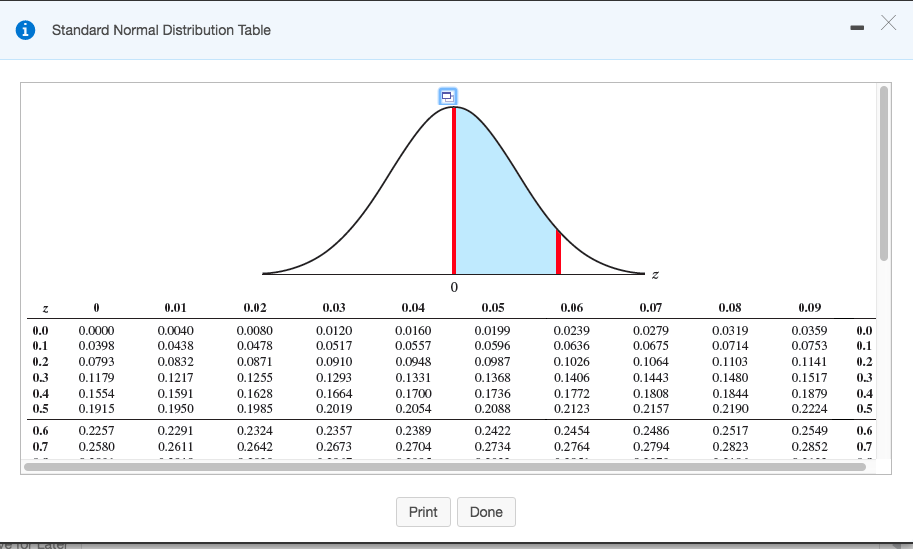

It will calculate the Standard Normal Distribution function for a given value. In Microsoft Excel or Google Sheets, you write this function as NORMSINV (0. This cheat sheet covers 100s of functions that are critical to know as an Excel analyst. Multiply this number by 100 to get percentages. Get an answer for Calculate the critical value of the standard Normal distribution associated with a confidence level of 96.4 given that only tabulated values for the 96th and 97th percentiles. Calculate right-tailed value: Since 0.055, the area under the curve is 1 - 1 - 0.055 0.945. Then go to the x axis to find the second decimal number (0.07 in this case). Find the first two digits on the y axis (0.6 in our example). Finding a corresponding probability is fairly easy. Since this number is greater than our alpha level of 0.05, we fail to reject the null hypothesis of our test. The p-value for a test statistic t of 1.34 for a two-tailed test with 22 degrees of freedom is 0.19392. Z-Score, also known as the standard score, indicates how many standard deviations an entity is, from the mean. In order to find this p-value, we can’t use the t distribution table because it only provides us with critical values, not p-values. For George’s example we need to use the 2nd table as his test result corresponds to a positive z-score of 0.67. A standard normal table (also called the unit normal table or z-score table) is a mathematical table for the values of, indicating the values of the cumulative distribution function of the normal distribution. If a z-score calculation yields a negative standardized score refer to the 1st table, when positive used the 2nd table. And then they tell us, what proportion of laptop prices are between 624 and 768. One standard deviation below the mean would put us right about there, and that would be 750 minus 60, which would be 690.
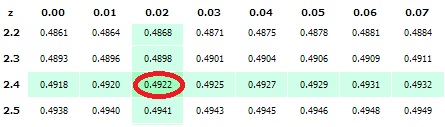
#Standard normal table for critical values plus
If you noticed there are two z-tables with negative and positive values. So that means one standard deviation above the mean would be roughly right over here, and that would be 750 plus 60. Standard normal distribution table) comes handy. Using the table of critical values for upper tailed tests, we can approximate the p-value. Therefore: Z score = (700-600) / 150 = 0.67 Now, in order to figure out how well George did on the test we need to determine the percentage of his peers who go higher and lower scores. A z-critical value is used when there is a normal sampling.


 0 kommentar(er)
0 kommentar(er)
